Om kryptografioppgavene
Disse oppgavene er strukturert litt annerledes enn de andre oppgavene på Piggy, lurer litt på hva dere foretrekker! 😎
Det kommer først til å være en del informasjon til å begynne med om temaene, deretter vil det komme noen oppgaver etterpå!
“Levlene” i denne oppgaven er ikke helt som levlene før, her er ting mer delt opp i temaer.
Hva er en “Cipher”?
Har du noen gang hatt lyst til å skrive en hemmelig beskjed til en venn, slik at ingen andre kan forstå den? Da trenger du et Cipher, eller chiffer på Norsk! Et chiffer er rett og slett en metode som gjør vanlig tekst om til “kode” ved å bytte ut tegn (ofte bokstaver) med andre tegn. Resultatet ser ut som tull for de som ikke vet hvordan koden fungerer. Poenget er at bare de som kjenner nøkkelen (regelen for å bytte ut bokstavene) kan gjøre koden forståelig igjen. Med andre ord: chiffer gjør hemmelige beskjeder mulig, enten det er barndommens lek med hemmelig språk eller ekte spioner som sender krypterte meldinger. 😄
Visste du?
Ordet “chiffer” stammer faktisk fra et arbisk ord: ordet sifr, som betyr “null”. Kanskje fordi den hemmelige koden så ut som ingenting (null mening!) når folk ikke kunne løse den!
Det finnes mange typer chiffer – noen bruker tall, noen bruker symboler, og moderne datakryptering bruker svært kompliserte algoritmer. Disse kompliserte algoritmene krever svært komplisert matematikk, så vi kan se på noen enklere algoritmer først!
Monoalfabetiske Chiffer
La oss først se på noen av de enkleste (og eldste) kodemetodene som finnes: monoalfabetiske chiffer.
Monoalfabetisk høres kanskje ut som et vanskelig ord, men vi kan dele det opp: mono betyr “én”, og alfabetisk handler om alfabetet.
Altså, monoalfabetiske chiffer er koder der man bruker ett enkelt “krypteringsalfabet” for hele meldingen. Det vil si at hver bokstav i den originale teksten alltid blir byttet ut med den samme bokstaven gjennom hele den krypterte meldingen.
For eksempel, har du bestemt at A skal byttes med X, da blir alle A-ene i teksten gjort om til X.
Cæsar-chiffer
Det klassiske eksempelet på et monoalfabetisk chiffer er Cæsar-chifferet (oppkalt etter Julius Cæsar). Dette er basically en regel om å “skifte” alle bokstavene et visst antall plasser bortover i alfabetet. Visstnok så brukte Cæsar selv et skifte på 3 bokstaver i sine hemmelige meldinger. Det fungerer sånn at A blir til D, B blir til E, C blir til F, og så videre gjennom alfabetet. (Når man går forbi Z, starter man på A igjen.) En melding som ABC ville dermed bli til DEF hvis vi bruker Cæsars metode.
Slik fungerer Cæsar-chifferet i praksis:
- Velg en nøkkel: Bestem deg for et hemmelig tall (for eksempel 3) som angir hvor mange plasser du skal flytte hver bokstav.
- Bytt ut hver bokstav: For hver bokstav i den originale meldingen, finn bokstaven som ligger så mange plasser etter den i alfabetet (for nøkkel 3 blir A til D, B til E, osv. – husk å gå rundt til A igjen etter Z om nødvendig). Eventuelt kan du også ta med Æ, Ø og Å, men dette blir litt mer komplisert.
- Kryptert melding: Erstatt bokstavene og skriv den nye meldingen med de “skiftede” bokstavene. Vips – du har en uleselig, hemmelig tekst som bare de med nøkkelen kan forstå!
- For å dekryptere (altså gjøre det om til leselig tekst igjen) gjør man bare det motsatte skiftet tilbake. Hvis du vet nøkkelen (f.eks. 3), så er det like lett å lese meldingen ved å flytte bokstavene 3 tilbake i alfabetet.
Sikkerhet?
Disse kodene er ikke særlig sikre i lengden. Fordi mønsteret (substitusjonen) er fast, kan en person med nok tålmodighet eller noen smarte triks fort avsløre hemmeligheten. For eksempel finnes det bare noen få mulige forskyvninger i Cæsar-chifferet, like mange som alfabetet, så hvem som helst kan prøve alle til meldingen gir mening – eller bruke bokstavfrekvenser til å gjette seg fram. Med andre ord, kanskje ikke bruk Cæsar-chifferet for superhemmelige dagboknotater eller statshemmeligheter 😉.
Monoalfabetiske chiffer er en fantastisk måte å lære prinsippet bak kryptering. De er enkle og viser hvordan vi kan bruke en enkel regel (en nøkkel) til å gjøre om en forståelig tekst til noe mystisk og uforståelig – og tilbake igjen. Så neste gang du vil sende en venn en hemmelig beskjed, kan du bruke Cæsar chifferet! Kanskje dere kan lage deres egen variant av Cæsars hemmelige alfabet? 🔐✨
Oppgaver
Programmeringsspråk?
Som før, bruke gjerne hvilket som helst programmeringsspråk du vil! Eksemplemene her vil være i Python.
 Oppgave 1.1 - Cæsar Chiffer Enkryptering
Oppgave 1.1 - Cæsar Chiffer Enkryptering
Nå skal vi faktisk skrive noe kode! Vi skal begynne enkelt med å lage enkrypteringen, basert på teorien bør det være ganske straightforward.
Implementer enkryptering med Cæsar Chiffer ved å bruke en funksjon som tar inn tekst og et tall som er “nøkkelen”, altså hvor mye alfabetet skal roteres med.
Tips til framgangsmåte.
- Lag en funksjon om heter
caesarsom tar inn teksten som skal enkrypteres og et “shift”, altså, hvor mange plasser i alfabetet teksten skal skiftes. - Gå i gjennom bokstav for bokstav i teksten.
- Vi vil ikke “shifte” andre tegn enn bokstaver: finn ut hvordan du sjekker at et tegn i teksten er en bokstav.
- Vi skal “rotere” bokstaven med n plasser, altså vi må legge til rotasjonen: finn ut hvordan du kan gjøre teksten om til tall slik at du kan legge til shiftet. Hint:
ord()funksjonen. - Husk! Her får du forskjellige verdier basert på om du har små eller store bokstaver. Referer til ASCII Tabellen.
- Etter du har en verdi er det så enkelt som å legge til n verdien. Men hva skjer dersom du er på slutten alfabetet? Vi får bare tull etter bokstaven Z. Hvordan fikses dette? Dette krever litt tenking.
Fikse enkrypteringen.
For å fikse krypteringen helt krever litt tenking.
- Det første steget å tenke på er bruk av modulus operatoren,
%. - Siden alfabetetet (på engelsk) består av 26 bokstaver, kan vi ta modulus med
26. - Men dette fungerer ikke helt, ser du grunnen?
- Prøv å
printut verdien til en karakter medord(), hva får du? - For
afår du 97. Hvis du tar modulus 26 med dette, får du 19. Husk at modulus vil alltid gi et svar mellom 0 og tallet. - Dette kan fikses ved å lagre startverdien til store og små bokstaver, trekke denne fra bokstaven, og deretter ta modulus. Da blir det:
(ord(bokstav) - ord('a')) % 26 - For å få tilbake den rette bokstaven legger du bare til startverdien igjen.
- Etter alt dette kan du endelig gjøre tallet om til en bokstav igjen. Her kan du bruke
chr()funksjonen. - Nå kan du endelig legge bokstaven til et resultat og returnere den enkrypterte teksten!
Løsning:
def caesar_cipher(text, shift):
result = ""
for char in text:
if char.isalpha():
# finn ut startpunktet basert på store og små bokstaver
start = ord('A') if char.isupper() else ord('a')
# Den vanskelige shifte-utregningen
result += chr((ord(char) - start + shift) % 26 + start)
else:
result += char
return result
 Oppgave 1.2 - Cæsar Chiffer Dekryptering
Oppgave 1.2 - Cæsar Chiffer Dekryptering
Dekryptering er bare å gjøre den motsatte utregningen til enkryptering. Du trekker fra offset i stedet for å legge til.
Tips til framgangsmåte.
Bruk funksjonen du lagde i oppgave 1 for dette. Bare ta samme funksjoen, men i revers. Dette kan du gjøre ved å gjøre shift om ved 26 - shift.
Løsning:
def caesar_decrypt(text, shift):
return caesar_cipher(text, 26 - shift)
Andre Monoalfabetiske Chiffer/Ciphers (ex. Atbash)
Det finnes andre monoalfabetiske chiffer også! En av de enklere er den som kalles “Atbash” Chiffer.
Hvordan fungerer Atbash?
Denne er svært enkel, i stedet for en rotasjon så kartlegges bokstaver til det motsatte alfabetet. Her er en tabell som viser kartleggingen:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| z | y | x | w | v | u | t | s | r | q | p | o | n | m | l | k | j | i | h | g | f | e | d | c | b | a |
 Oppgave 1.3 - Atbash Chiffer Enkryptering og Dekryptering
Oppgave 1.3 - Atbash Chiffer Enkryptering og Dekryptering
Det kjekke med Atbash er at siden enkryptering er en 1 til 1 transformering, så fungerer den direkte i revers. Altså, hvis du har lagd enkrypteringen så har du også, automatisk lagd dekrypteringen.
Hvordan kan dette gjøres i praksis?
Du kan enten trekke fra bokstaven i forhold til Z, eller lage en “Look-up” table. Altså, det betyr en tabell eller dictionary som inneholder alle bokstavene fra a til z og hva de skal bli. Dette kan være god løsning hvis dere vil lage en annen type enkryptering.
Lookup-table implementasjon.
letters = {
'a': 'z'
'b': 'y'
'c': 'x'
'd': 'w'
# ... legg til resten av bokstavene nedover
}
Ved hjelp av denne tabellen kan du gå igjennom bokstav for bokstav, så hente ut verdien per bokstav fra lookup-tabellen, så skrive den ut. Hva må du gjøre for store og små bokstaver?
Del 2 - Kryptoanalyse av Monoalfabetiske Chiffer
I denne delen skal dere prøve å lage en algoritme for å “cracke” en Cæsar chiffer, altså ta en kryptert tekst, deretter, få ut den orginale teksten uten å vite nøkkelen.
Dette kan gjøres noenlunde manuelt, eller så kan du prøve å ta i bruk enkel “cryptanalysis”. Dette er et konsept som vi skal se dypere på senere, men for nå skal vi bare se på en av de enkleste måtene: Frekvensanalyse (frequency analysis). Du kan lese mer om dette konseptet her: Frequency Analysis eller her Wikipedia - frequency analysis.
Denne metoden kan brukes i mer en bare cæsar-chiffer, den kan brukes i mer kompliserte algoritmer også, men cæsar-chiffer er såpass enkel at frekvensanalyse er trivielt.
Hvordan fungerer frekvensanalyse?
Frekvensanalyse er, som navnet hinter på, en måte å sjekke frekvensen av bokstaver i en tekst. Hvorfor kan dette være nyttig? Se for deg at du har en lang tekst, vi skal se for oss en engelsk tekst, hentet fra Wikipedia - frequency analysis:
In cryptanalysis, frequency analysis is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers.
Frequency analysis is based on the fact that, in any given stretch of written language, certain letters and combinations of letters occur with varying frequencies. Moreover, there is a characteristic distribution of letters that is roughly the same for almost all samples of that language. For instance, given a section of English language, E, T, A and O are the most common, while Z, Q, X and J are rare. Likewise, TH, ER, ON, and AN are the most common pairs of letters termed bigrams or digraphs), and SS, EE, TT, and FF are the most common repeats. The nonsense phrase ETAOIN SHRDLU represents the 12 most frequent letters in typical English language text.
In some ciphers, such properties of the natural language plaintext are preserved in the ciphertext, and these patterns have the potential to be exploited in a ciphertext-only attack.
Dersom vi tar å gjør denne teksten om ved Cæsar chiffer (også tar vi vekk komma, mellomrom og andre spesielle karakterer), får vi følgende chiffer-text:
xcrgneipcpanhxhugtfjtcrnpcpanhxhxhiwthijsnduiwtugtfjtcrnduatiitghdgvgdjehduatiitghxcprxewtgitmiiwtbtiwdsxhjhtsphpcpxsidqgtpzxcvraphhxrparxewtghugtfjtcrnpcpanhxhxhqphtsdciwtupriiwpixcpcnvxktchigtirwdulgxiitcapcvjpvtrtgipxcatiitghpcsrdbqxcpixdchduatiitghdrrjglxiwkpgnxcvugtfjtcrxthbdgtdktgiwtgtxhprwpgpritgxhixrsxhigxqjixdcduatiitghiwpixhgdjvwaniwthpbtudgpabdhipaahpbeathduiwpiapcvjpvtudgxchipcrtvxktcphtrixdcdutcvaxhwapcvjpvttippcsdpgtiwtbdhirdbbdclwxatofmpcsypgtgpgtaxztlxhtiwtgdcpcspcpgtiwtbdhirdbbdcepxghduatiitghitgbtsqxvgpbhdgsxvgpewhpcshhttiipcsuupgtiwtbdhirdbbdcgtetpihiwtcdchtchtewgphttipdxchwgsajgtegthtcihiwtbdhiugtfjtciatiitghxcinexrpatcvaxhwapcvjpvtitmixchdbtrxewtghhjrwegdetgixthduiwtcpijgpaapcvjpvteapxcitmipgtegthtgktsxciwtrxewtgitmipcsiwthtepiitgchwpktiwteditcixpaidqttmeadxitsxcprxewtgitmidcanpiiprz
Denne teksten ser jo umulig ut å “cracke”, men ved hjelp av “Frekvens-analyse” er det ikke bare mulig, men enkelt.
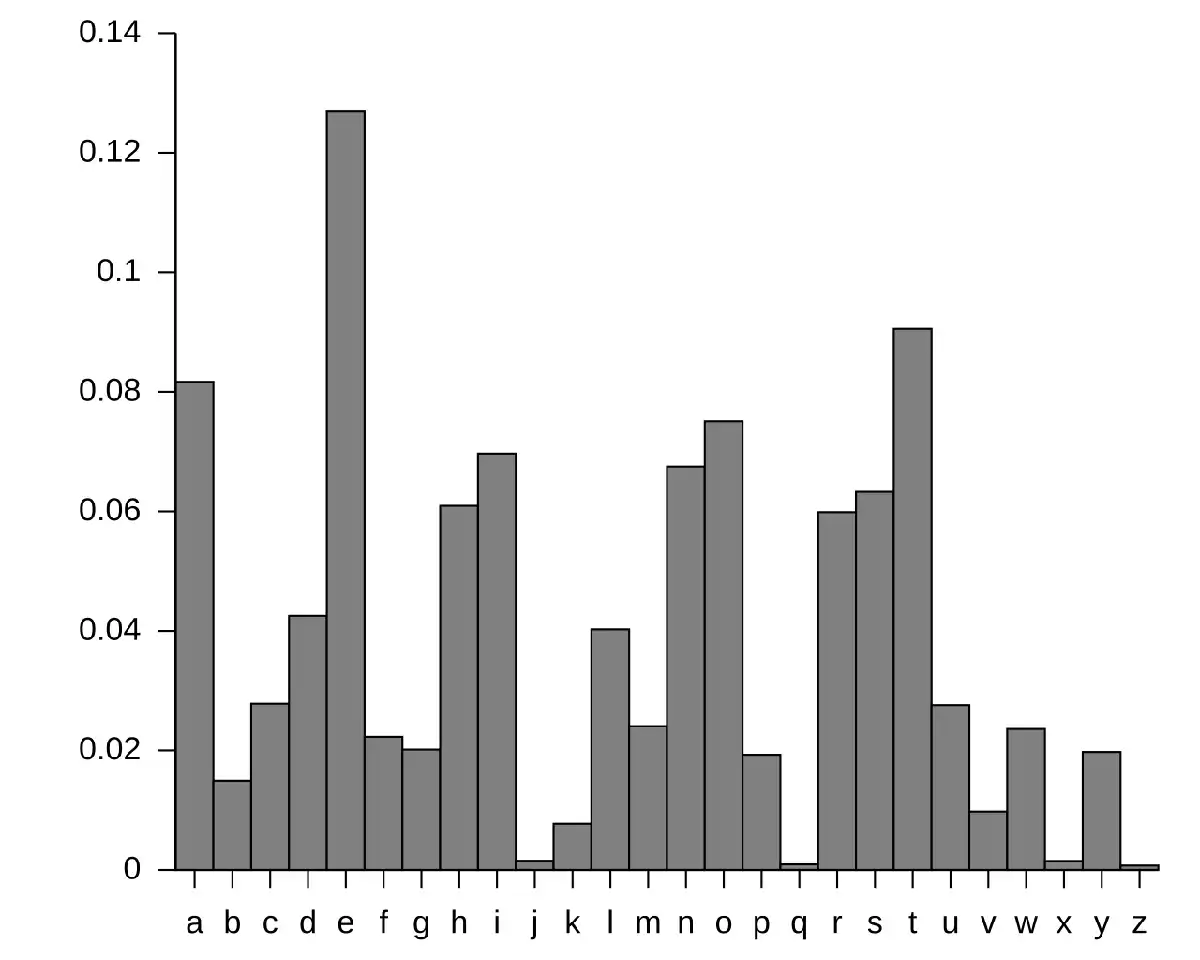
Dette er en figur som viser distribusjonen av bokstaver på engelsk. Det vi kan se, er at bokstaven E er den hyppigste bokstaven, etterfulgt av T, A og O.
Denne kan gjøres om til en tabell og så brukes til å telle og analysere en gitt chiffer-tekst for så å “cracke” den. I oppgavene under skal du lage et program som kan “cracke” ceasar chiffer på egenhånd. Det er sant at cæsar-chifferet er så enkelt at du kan bare sjekke alle 26 mulighetene manuelt, men her skal vi finne ut løsningen, helt automatisk.
 Oppgave 2.1 - Lage en frekvenstabell
Oppgave 2.1 - Lage en frekvenstabell
I en python fil, opprett en frekvens-tabell av bokstavene i det engelske språket. Du kan prøve å finne denne selv, men hvis du ikke gidder dette, forstår vi dette!
Hvis du absolutt ønsker å finne den selv, kan du gjøre som i Oppgave 2.2, men på en veldig stor tekst.
English Letter Frequency (Svaret)
english_letter_frequency = {
'E': 12.70,
'T': 9.06,
'A': 8.17,
'O': 7.51,
'I': 6.97,
'N': 6.75,
'S': 6.33,
'H': 6.09,
'R': 5.99,
'D': 4.25,
'L': 4.03,
'C': 2.78,
'U': 2.76,
'M': 2.41,
'W': 2.36,
'F': 2.23,
'G': 2.02,
'Y': 1.97,
'P': 1.93,
'B': 1.29,
'V': 0.98,
'K': 0.77,
'J': 0.15,
'X': 0.15,
'Q': 0.10,
'Z': 0.07
}
 Oppgave 2.2 - Telle frekvensen av bokstaver i tekst
Oppgave 2.2 - Telle frekvensen av bokstaver i tekst
Nå skal vi lage en algoritme som skal finne frekvensen av bokstaver i en gitt tekst.
Tips til framgangsmåte
- Begynn med en funksjon som tar inn en tekst (kan være hva som helst).
- I funksjonen, opprett en “dictionary” (Python Dictionaries), med entries for hver bokstav i alfabetet, satt til
0. ({'A' = 0, 'B' = 0, 'C' = 0, ..., 'Z' = 0}) - Gå igjennom hele teksten og tell hver eneste bokstav (øk med 1 i tilsvarende entry i dictionariet). Her bør du nok ignorere tegn som ikke er bokstaver, husk også store og små bokstaver.
- Hold styr på hvor mange bokstaver som har blitt telt totalt.
- Når du er ferdig med å telle, del
/hver verdi i tabellen med lengden av teksten og så gange med 100, dette vil gi deg en prosent-frekvens. (Du kan selvfølgelig heller la tabellen din over være mellom 0 og 1). - Nå skal du ha en frekvens-tabell for teksten.
 Oppgave 2.3 - Sammenligne frekvensen av en tekst med den ekte frekvensen
Oppgave 2.3 - Sammenligne frekvensen av en tekst med den ekte frekvensen
Når du har funnet frekvensen til alle bokstavene i teksten kan du lage en funksjon som finner “avstanden”. Hæ? Hva menes med det?!
Du kan se for deg at frekvensen til for eksempel E i teksten kommer til å være et tall. Du kan finne “avstanden” denne har med den faktiske frekvensen, som er 12.70. Eksempel: Frekvensen er 9.63, hva er avstanden? Avstanden kommer til å være den absolutte verdien (negative tall blir positive) mellom disse to verdiene: \(12.70 - 9.63 = 3.07\).
Lag en funksjon som går igjennom hver av bokstavene å finner avstanden. Legg deretter alle avstandene sammen til en “total” avstand.
Mattefunksjon?
Hvis du lurer på hvordan matte-funksjonen for denne er, så ser den slik ut:
\(\sum_{n=0}^{N} \lvert a - b\rvert\)
Tips til framgangsmåte
- Bruk en
for-loop til å gå igjennom hele frekvens-tabellen. - For hver bokstav i frekvenstabellen, finn absolutt-verdien sammenlignet med den faktiske frekvensen. Bruk
abs()funksjonen i Python for dette. - Legg sammen alle verdiene, så skal du få et slutt-resultat.
 Oppgave 2.4 - “Cracke” Cæsar-chiffer
Oppgave 2.4 - “Cracke” Cæsar-chiffer
Nå skal vi til slutt sette sammen alt vi har gjort så langt! Nå skal vi “cracke” en Cæsar-chiffer.
Lag et program som “cracker” en Cæsar-chiffer! Uten bruker-innflytelse skal du kunne hive inn en kryptert tekst å hente ut den dekrypterte teksten uten å trenge en nøkkel.
Test data
Her er noe test-data dere kan bruke, hva sier disse?
| Test-data |
|---|
cqrbvnbbjpnrbjenahbnlancxwnqxynoduuhhxdjanjkuncxmnlxmnrclxvyuncnuhjwmqnanjanbxvnfxamboaxvxdaojexarcnsnmrqnuuxcqnanrcbxenajwjtrwrqjencqnqrpqpaxdwmhxdfnanarpqccqnwnpxcrjcrxwbfnanbqxac |
lsaizivxlmwqiwwekimwuymxiwlsvxwsmxqmklxrsxasvoewibtigxihlsaizivmjmxhsiwksshnsf |
bmtxymjwjsfdfsxbjwrjxyfsifsizsktqidtzwxjqkqtslqnajymjpnslgfwsfwitmjdtzhtrjrtxyhfwjkzqqdzutsdtzwmtzwynxstbxywzhpybjqajljyymjjytgjikwfshnxhtktwymnxwjqnjkrzhmymfspxynxgnyyjwhtqifsinfrxnhpfymjfwymfajdtzmfivznjylzfwistyfrtzxjxynwwnslbjqqlttisnlmynkdtzitrjjymtwfyntfsirfwhjqqzxymjwnafqxtkrdbfyhmgniymjrrfpjmfxyj |
zwkyvivrivrepzuzfkjzekyviffdnzcckyvpgcvrjvjkreulgjrzukyvjritrjkztkvrtyvirwkvircfexjzcvetvfevwivjydreifjvkfyzjwvvkefnkyvedzjkvinypufpfltfejzuvipflijvcwrezuzfkzehlzivukyvkvrtyvinzkyrjevvinvccrtklrccpzufekjrzukyvjkluvekslkzyrkvkfjvvpfljkreuzexlgkyvivrccsppflijvcw |
uwwilxchaniuffehiqhfuqmizupcuncihnbylycmhiqusuvyymbiofxvyuvfynizfscnmqchamulyniimguffniayncnmzunfcnnfyvixsizznbyaliohxnbyvyyizwiolmyzfcymuhsqusvywuomyvyymxihnwulyqbunboguhmnbchecmcgjimmcvfysyffiqvfuwesyffiqvfuwesyffiqvfuwesyffiqvfuweiibvfuweuhxsyffiqfynmmbueycnojufcnnfyvullsvlyuezumncmlyuxswigcha |
Tips til framgangsmåte
- Begynn med å lage en funksjon som tar inn tekst.
- Bruk dekrypterings-funksjonen for Cæsar-chiffer med rotasjon N på teksten, N begynner på 0.
- Lag en frekvenstabell av resultatet
- Finn ut avstanden til resultatet i forhold til den faktiske frekvenstabellen
- Enten: a) hold styr på avstanden i en liste, eller b) hold styr på den minste verdien og rotasjonen (dette blir nøkkelen)
- Øk rotasjonen med 1 og repeter steg 2 til 6 helt til N når 26 (full rotasjon).
- Returner den dekrypterte teksten, altså den minste-avstanden er den rette nøkkelen.